ReLU関数 (4/5) ReLUの改良案
はぐれ弁理士 PA Tora-O です。前回(第3回)では、活性化関数の要求仕様を踏まえてクレーム第2形態を作成しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。
今回(第4回)は、ReLUの改良案、言い換えれば迂回技術を例示しつつ、クレームの妥当性についてレビューを実施します。まずは、評価対象のクレームを挙げておきましょう。
【クレーム骨子】(前回より再掲)
複数の演算ユニットを含んで構成されるニューラルネットワークを用いた演算方法であって、少なくとも1個の演算ユニットの活性化関数が、以下の2つの条件A,Bを同時に満たすことを特徴とする演算方法。
(条件A)全区間内に少なくとも1つの屈曲点があること。
(条件B)屈曲点から正側に延びる直線の傾きが1であること。
改良案その1:Leaky ReLU
ReLUでは、負の区間における出力を一切無効(F(x)=0)にします。例えば、活性化を抑制させる因子(実際のニューロンにおけるGABAの発火抑制効果)を加えた方が、学習時の収束性がより高まるかもしれません。そこで、図1に示すようなLeaky ReLUが提案されました。ちなみに、この関数における負側の傾きは 0.01 とかなり小さな値に設定されています!関数式は、F(x)=max(x,0.01x)となります。
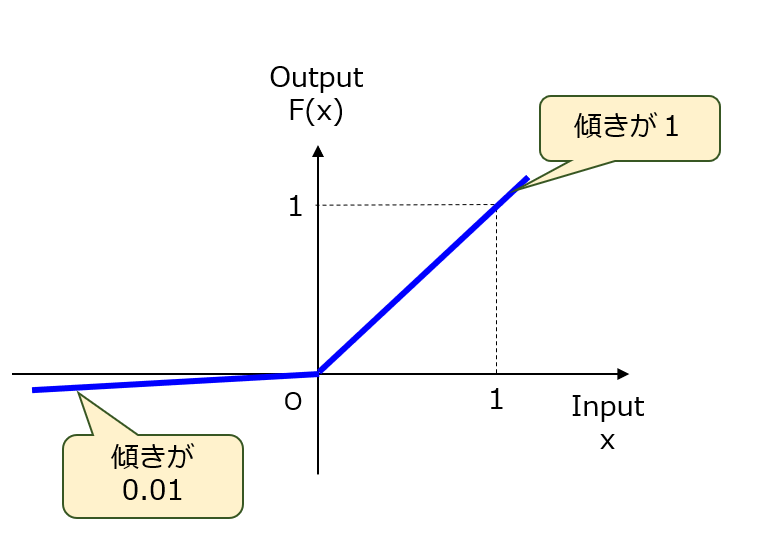
【図1】Leaky ReLU
これに対して、上記したクレームでは、負の区間における関数の形状的特徴を一切規定していません。つまり、1以外であれば、負側の傾きが(1)0、(2)正、(3)負、のいずれの関数であってもクレーム範囲に含まれます。結論として、改良案その1についてカバー済み(OK判定)という評価になりました。
なお、Leaky ReLUの類型には、PReLU(Parametrized ReLU)、RReLU(Randomized ReLU)などがあります。これらの名称だけで関数の特徴が何となく理解できるでしょう。
改良案その2:ELU
ReLUでは、屈曲点x=0で滑らかになっていません。例えば、全区間にわたって滑らかな関数である方が、一次微分関数も連続である分だけ学習時の収束性がより高まるかもしれません。そこで、図2に示すようなELU(Exponential Linear Unit)が提案されました。要は、ELUとは、x=-∞でy=-a(aは正値)に収束するtanh関数を用いて、直線の一端(0,0)を滑らかに接続した関数です。
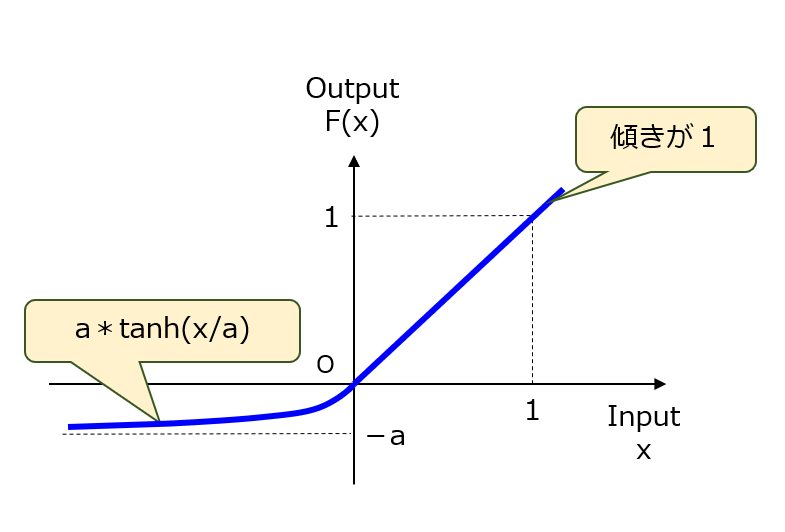
【図2】ELU
これに対して、上記したクレームでは、「屈曲点」と記載されているので、屈曲点がないELUはクレーム範囲から外れます。結論として、改良案その2についてカバー未了(NG判定)という評価になりました。ただし、クレーム表現をもう少し工夫すれば何とか対応できそうな感じでしょうか。
改良案その3:ReLU6
ReLUでは、正の区間において入力値の増加に応じて出力値も増加していきます。例えば、従来型の活性化関数のように、適切な上限値でクリッピングすれば、学習時の収束性がより高まるかもしれません。そこで、図3に示すようなReLU6(×ロト6)が提案されました。この「6」は経験則的に定められた上限値であり、ReLU100,056であっても構いません。
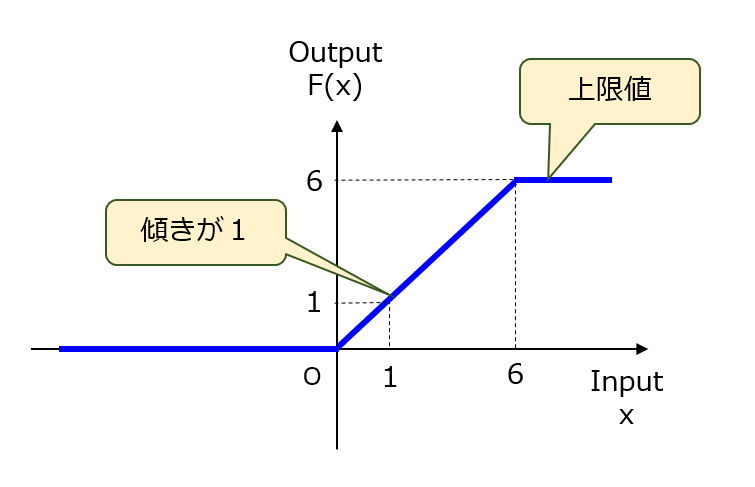
【図3】ReLU6
これに対して、上記したクレームでは、「直線」と記載されているので、正側に無限に延びる傾き1の直線を有さないReLU6はクレーム範囲から外れます。結論として、改良案その3についてもカバー未了(NG判定)という評価になりました。ただし、こちらの方も、クレーム表現をもう少し工夫すれば何とか対応できそうな感じです。
なお、ReLU6の類型には、ハードシグモイド(Hard Sigmoid)や、Htanh(Hard Hyperbolic Tangent)などがあります。ハードシグモイドは、ReLU1の直線傾きを1から0.2に変更し、かつX軸負方向に2.5だけ平行移動した関数に相当します。また、Htanhは、ReLU±1に相当し、max{-1,min(x,1)}の関数式で表されます。
以上、今回(第4回)は、クレーム第2形態のレビューを実施しましたが、どうやらまだ完全体ではなかったことが判明しました。テーマ最終回(第5回)は、今まで4回分の総括と、この事例検討の所感を述べたいと思います。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。








ディスカッション
コメント一覧
まだ、コメントがありません