Word2Vec（4/4）クレーム骨子の作成
はぐれ弁理士 PA Tora-O です。前回（第３回）では、“Skip-gram” モデルの概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回（第４回）は、これまでの検討を踏まえ、クレーム骨子を作成してみます。
技術的特徴の認定
クレームの作成に先立ち、本発明に相応しい先行技術を認定することが必要になります。しかし、色々と調べてみたのですが、実際の先行技術がどれであるか特定できませんでした。そこで、今回は、先行技術との相違点の有無に拘らず、ワンホット表現から分散表現に変換する方法について、２種類のモデルを包含するクレームを作ってお茶を濁そうと思います。
分散表現（Distributed Representation）とは、複数の連続値成分を組み合わせたベクトルを用いて単語を定量化する手法です。この表現により、単語群を構成する単語数に依存しない表現ができること、単語の一致性のみならず単語同士の関係性を定量化できること、などのメリットが生じます。それでは、“Word2Vec”（分散表現）のクレーム骨子は、以下の通りです。
クレーム骨子
【クレーム】（Word2Vec）
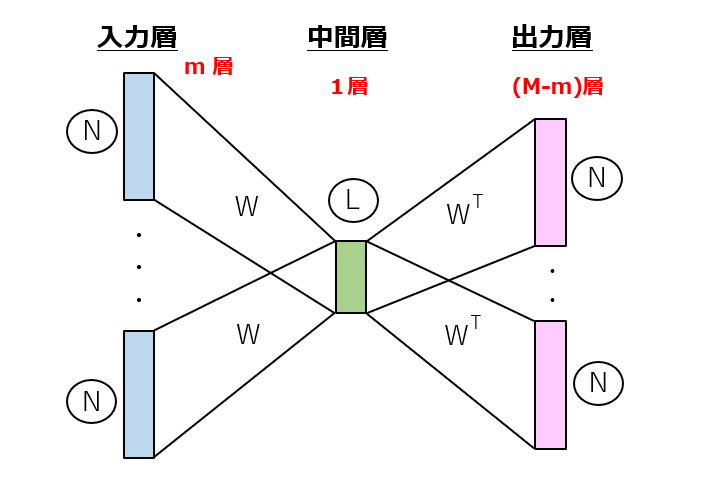
Ｎ個の単語からなる単語群の分散表現を行う方法であって、
［１］単語のラベル集合を入力するＮ個の演算ユニットからなるｍ層の入力層、
［２］１≦Ｌ＜Ｎの関係を満たすＬ個の演算ユニットからなる１層の中間層、及び
［３］単語のラベル集合を出力するＮ個の演算ユニットからなる（Ｍ－ｍ）層の出力層
が全結合により順次接続されたニューラルネットワークを用いて、Ｍ個の連続する単語同士の関係性を学習するステップと、
学習を通じて決定された入力層または出力層と中間層との間の結合重み行列から、連続値の成分を有するＬ次元のベクトルを単語毎に求めるステップと、
を備えることを特徴とする分散表現方法。（２８３文字）
ポイント解説
分散表現
発明の意図を明確にするためにこの文言を加えています。技術用語として曖昧さを感じるようであれば削除しても全く問題ありません。
ｍ層の入力層／（Ｍ－ｍ）層の出力層
理論的には、入力層が１層以上、出力層が１層以上であれば、連続する単語数や配列の順位を色々組み合わせても良さそうです。
１≦Ｌ＜Ｎ
次元削減の概念を不等式で表現しています。
全結合により
結合重みの個数がＮ・Ｌ個になるためには必須の構成です。この文言に代えて、結合重み行列が（Ｎ×Ｌ）または（Ｌ×Ｎ）であることを明示してもＯＫです。
入力層または出力層と中間層との間
入力側の（Ｎ×Ｌ）行列から「各行」を抜き出す方法の他に、出力側の（Ｌ×Ｎ）行列から「各列」を抜き出す方法もあり得ます。また、複数の結合重み行列に対して統計処理（例えば、平均化）を施し、１つの結合重み行列を求めても構いません。
以上をもちまして、”Word2Vec” の事例検討を終了します。次回から、また別のテーマに移ります。
↓ブログランキングに参加しています。よろしければ１クリックお願いします。
