ReLU関数 (1/5) 発明の概要
はぐれ弁理士 PA Tora-O です。今回のテーマとして、ディープラーニングで頻出のReLU関数を題材に取り上げていきます。
背景
例えば、教師あり学習では、出力値と教示値の差分の関数である損失関数(あるいは、学習誤差)が大局的最小値になる学習パラメータセットを求め、その最小値に近づくように学習パラメータセットを逐次更新していきます。これらの厳密解(Exact Solution)を求める場合、超多次元の連立方程式を解かなければならず、これだけでも演算時間が膨大になってしまいます。
そこで、ディープラーニング(DL)における学習パラメータの更新手法として、誤差逆伝播法(Back Propagation)がよく用いられます。この手法は、入力→出力の流れとは逆方向に(出力→入力の流れで)更新量が計算される点に特徴があり、厳密解を求める場合と比べて、更新に要する計算量が大幅に削減されるというメリットがあります。
問題の所在
ところが、この誤差逆伝播法を用いて結合重みを更新する際、勾配消失(Vanishing Gradients)が大きな問題になります。「勾配消失」とは、逆伝播の過程において誤差の勾配が消失し、入力層付近での学習が進みにくくなるDL特有の問題を意味します。この現象は、ネットワークの階層が深くなるにつれて、より顕在化することが容易に想像できます。
解決手段
この勾配消失問題に対する1つのブレイクスルーになり得たのは、活性化関数(Activation Function)の見直しです。「活性化関数」とは、個々の演算ユニットが有する入出力特性に相当します。元々、この入出力特性はニューロンの伝達特性(つまり、ニューロン内の膜電圧に対する発火頻度の関係)を意味することから、一昔前では伝達関数(Transfer Function)の呼称の方がメジャーな表現だったような気がします。
この古典的な「伝達関数」には、図1に示すような、マカロック-ピッツ(McCulloch & Pitts)が提案した階段関数(Step Function)や、統計力学の基本理論であるイジングモデルの名残とも言える双曲線正接関数(Hyperbolic Tangent Function)が用いられてきました。ちなみに、この分野では有名なシグモイド関数(Sigmoid Function)は、単に、tanh関数の出力値(-1~+1)をリスケール(0~+1)したものです。
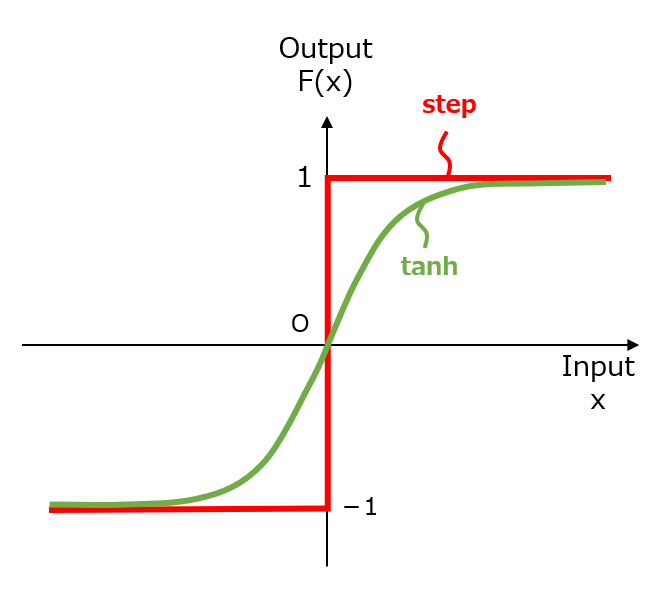
【図1】古典的な伝達関数
一方、新たに提案されたReLU(Rectified Linear Unit)関数とは、図2のような形状を有しています。他の工学分野では、ランプ関数(Ramp Function)と呼ばれているそうです。
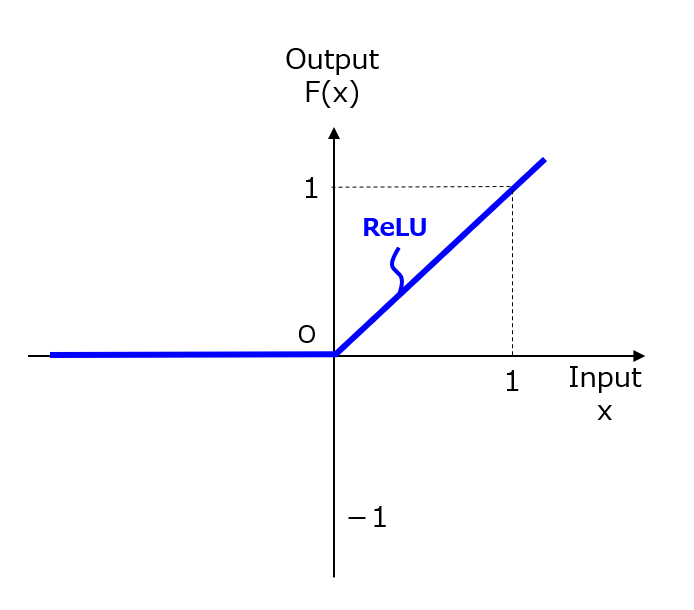
【図2】ReLU関数
そして、クレーム骨子は、次のようになります。
【クレーム骨子】(第1形態)
複数の演算ユニットを含んで構成されるニューラルネットワークを用いた演算方法であって、少なくとも1個の演算ユニットの活性化関数F(x)が、F(x)=max(x,0)であることを特徴とする演算方法。
以上をもちまして、ReLU関数の事例検討を終了します。・・・・・と言ったら何も面白くないので、次回以降、残り4本分の記事を捻り出していきます。ここが、AI派弁理士としての腕の見せ所です。
なお、この技術をさらに詳しく知りたい方は、例えば、「活性化関数」&「ReLU」で検索してください。次回(第2回)は、活性化関数の要求仕様について検討していきます。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。









ディスカッション
コメント一覧
まだ、コメントがありません