ReLU関数 (2/5) 活性化関数の要求仕様<前半>
はぐれ弁理士 PA Tora-O です。前回(第1回)では、ReLU関数の概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。
今回(第2回)は、活性化関数の要求仕様について、ReLUをベースに検討します。なお、今回の内容は、過去の論文や専門書の内容をすべて把握した上で記載したものではなく、あくまでも自らの知識や知見に基づいて記載したものです。そのため、技術的に正確さを欠く部分もありますが、発明の本質部分を捉えるための1つのアプローチとして参考にしていただければ幸いです。
それでは本題に入ります。長々と説明すると却って解りにくくなりますので、まず結論から述べた上で、個々の要件について理由とともに解説していきます。活性化関数が満たすべき要件として、次の3つを定義しました(図1)。
- 連続関数であって広義単調増加であること。
- 全区間線形性が破れていること。
- 活性化区間における傾きが1であること。
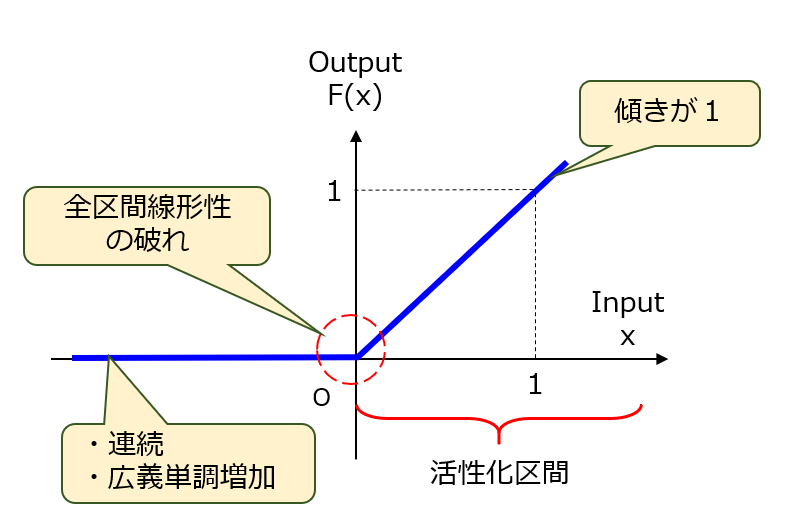
【図1】活性化関数の要求仕様
第1要件 連続かつ広義単調増加
活性化関数の出力は、連続値または離散値のいずれであっても特に問題ありません。が、昔と比べてコンピュータの性能上の制約がなく、演算の高速化やメモリの節約などのためにあえて離散化する必要はありません。そこで、第1要件として、活性化関数が全区間にわたって連続であることを挙げておきます。ただし、活性化関数が滑らかである必要はありません。言い換えれば、1次微分関数が部分的に不連続(ReLUの場合、x=0)であっても可です。
また、活性化関数をより複雑な形状にすると、損失関数における偽の最小値(Spurious Minima)を多発させる要因となり、その分だけ学習の収束性を損なう可能性があります。そこで、活性化関数が全区間にわたって減少しないこと、つまり広義単調増加、あるいは単調非減少であることも念のため要件に加えておきます。
第2要件 全区間線形性の破れ
この「全区間線形性」は自作の造語です。この語は、全区間において線形性を有すること、つまり、全区間において単体の1次関数のみで表現できることを意図します。具体的には、恒等関数(F(x)=x)などがこれに該当します。例えば、すべての演算ユニットの活性化関数が恒等関数である場合、個々の演算ユニットにおいて線形的な演算が行われます。結局、ネットワークの階層を幾ら深くしても、システム全体として単純な演算(つまり、簡単な学習)しか行えず、より高次の学習を実現することができません。
これを防ぐため、全区間線形性の破れがある活性化関数を選択する必要があります。最も解りやすい例として、前回に述べたtanh関数やシグモイド関数のような非線形関数が挙げられます。 ところで、ReLU関数のような折れ線関数は、全区間線形性あり/なしのどちらに該当するのでしょうか?確かに、正の区間では線形性(y=x)がありますが、屈曲点(x=0)の前後にわたる区間では線形性が失われています。したがって、ReLU関数は全区間線形性がないと言えます。
第3要件 活性化区間での傾きが1
誤差逆伝播法で採用される勾配降下法によれば、学習パラメータ(例えば、結合重みω)の更新量は、損失関数(L)を当該結合重み(ω)で偏微分した量(∂L/∂ω)に比例します。そして、具体的な説明は他のブログや専門書に譲りますが、図2のように誤差逆伝播法では、チェーンルール(偏微分のカスケード則)を利用しつつ、出力側から入力側に向かって、結合重みの更新量が逐次的に計算されます。
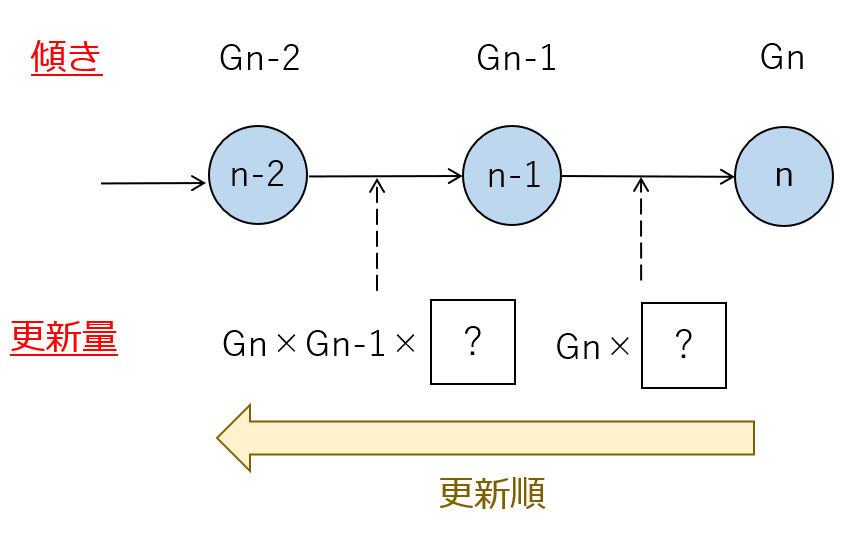
【図2】結合重みの更新イメージ
本検討に必要な部分のみを説明すると、各々の結合重みの更新量は、出力側から入力側に向かってパスを構築する際に、そのパスを構成するノードである演算ユニットの関数傾きの総乗(プロダクト)に比例するということです。例えば、(n+1)個の演算ユニットを繋ぐパスを構築する場合、このプロダクトは、Gn×Gn-1×・・・×G1に相当します。
つまり、入力側に近い結合重みほど、更新量に乗算されるプロダクトの項数が増えることになります。特に、結合重みがそれぞれ1より小さい場合には、項数の増加につれてプロダクトが減衰します。そう、お察しの通り、この減衰が勾配消失を引き起こす原因になっています。これに対して、階層の深さや入力値(正の範囲に限る)にかかわらずプロダクトを一定に保てるように、関数の傾きが1であることが重要です。そこで、ReLU関数の登場に繋がります。
それでは何故、今まで、活性化関数としてtanh関数やシグモイド関数が主に使われ続けてきたのでしょうか?ここからは私見ですが、ニューラルネットワークの研究目的がそもそも人間の脳のメカニズムを解明することにあったためと推測されます。つまり、実際のニューロンには発火頻度の上限があるという自然現象をそのまま固定観念として受け入れた結果、ReLU関数のような機械的?な発想になかなか至らなかったのかもしれません(と勝手に解釈しています)。疲れを知らず際限なく発火できるニューロン、如何にも人工的という感じがします。
以上、今回(第2回)は、活性化関数の要求仕様について説明しました。次回(第3回)は、その続きを説明し、改めてクレーム骨子を作成してみます。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。











ディスカッション
コメント一覧
まだ、コメントがありません