Negative Sampling(2/4)具体的な実施例
はぐれ弁理士 PA Tora-O です。前回(第1回)では、“Negative Sampling” の概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。
今回(第2回)は、“Negative Sampling” の具体的な実施例について、前回【図3】の「目的関数算出部」の機能を中心に説明していきます。
計算成分の選択
目的関数の計算に先立ち、N個の演算ユニット(NL本の結合重み)の中からn個(nL本)を選択します。先に述べた「ドロップアウト」では、確率がp= (n/N) となるように、N個の母集団の中からn個をランダムに抽出します。また、この確率(p)は、例えばp=0.5 と、それなりに大きい値に設定されます。
これに対して、“Negative Sampling” では、[1]1個の正例を必ず選択し、[2]確率がp=(n-1)/(N-1) となるように、残り(N-1)個の母集団の中から(n-1)個の負例をランダムに抽出します(図1)。
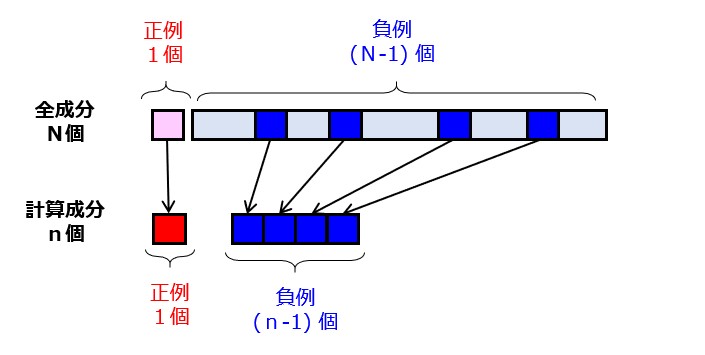
ここで、正例(Positive Example)とは “one-hot vector” の成分値が「1」である単語を意味し、負例(Negative Example)とは “one-hot vector” の成分値が「0」である単語を意味します。このようにして、N個の演算ユニットのうちのn個が有効化されるとともに、残りの(N-n)個が無効化されます。ここで、n≪N を満たすため、確率(p)が0に近い微小値に設定される点にも留意しましょう。
目的関数の計算
次に、選択した演算ユニットからのn個の出力値{Oi}を用いて、nL本の結合重みに関する更新量を決定するための目的関数(ここでは、損失項のみ)を計算します。“Word2Vec” では、出力側の活性化関数がソフトマックス(出力値が[0,1]の確率)であるため、損失項にはこの類の回帰問題に適した交差エントロピー(Cross Entropy)が選択されます。
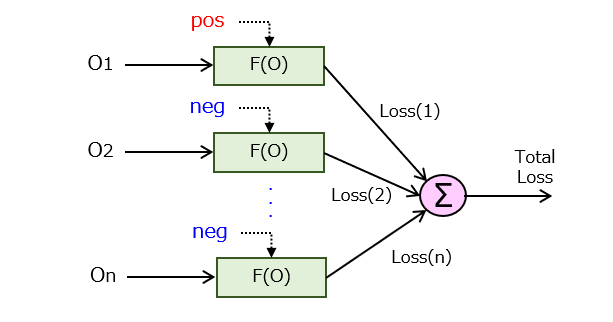
図2に示すように、出力値毎の損失を求め、n個の損失を加算することで、システム全体の損失項(つまり、目的関数)を計算します。ここで、F(・) は損失関数であり、図3に示すように、正例(pos)であるか負例(neg)であるかに応じて関数形が切り替わります。
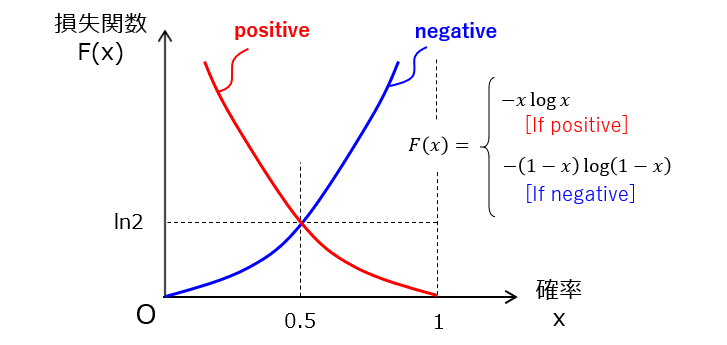
正例タイプの関数では、正解x=1 の場合に損失が最小(Loss=0)になり、不正解x=0 に近づくにつれて損失が単調に増加していきます。一方、負例タイプの関数では、正解x=0 の場合に損失が最小(Loss=0)になり、不正解x=1 に近づくにつれて損失が単調に増加していきます。
結合重みの更新
最後に、誤差逆伝播法(Backpropagation)により、上記した目的関数を用いて(nL)本の結合重みを更新します。ここでは、オンライン学習の例を説明しましたが、バッチ学習あるいはミニバッチ学習であっても構いません。
以上、今回(第2回)は、“Negative Sampling” の実施例について説明しました。次回(第3回)は、ドロップアウトとの相違点を念頭に入れつつ、“Negative Sampling” 特有の作用効果について考察してみます。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。









ディスカッション
コメント一覧
まだ、コメントがありません