正則化(2/4)実施例の検討
はぐれ弁理士 PA Tora-O です。前回(第1回)では、正則化の概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回(第2回)は、正則化の実施例を具体的に検討したいと思います。
典型的な実施例
前回も述べた通り、正則化項は、学習パラメータセットのスパース化を促進させる項に相当します。よく知られている手法は、以下の3種類です。
- L1正則化(LASSO回帰)
- L2正則化(Ridge回帰)
- Elastic-Net正則化
これらの目的関数は、次のように記述されます。Fは目的関数、Lは損失項、λ1,λ2は正のハイパーパラメータを示しています。なお、λ1,λ2=0を満たす場合、正則化が行われません。
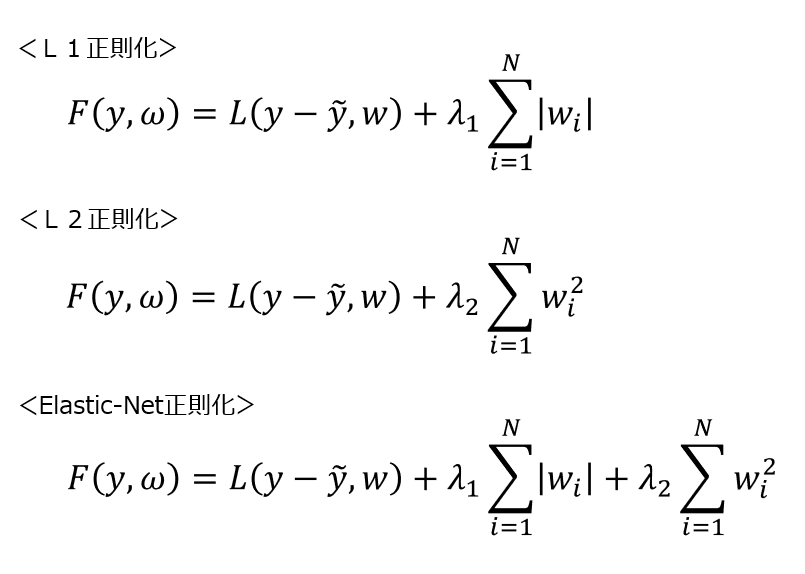
【数式1】3種類の目的関数
L1正則化は、L1ノルムを用いたアルゴリズムであり、この正則化項は|W|に比例して増加する1次関数です。L2正則化は、L2ノルムを用いたアルゴリズムであり、この正則化項は|W|の2乗に比例して増加する2次関数です。Elastic-Net正則化は、L1正則化とL2正則化を折衷させたアルゴリズムであり、この正則化項は|W|に関する一対の2次関数を結合した関数です。
なお、Pythonの機械学習ライブラリ”scikit-learn”において、上記した正則化に関するクラスがそれぞれ定義されています。
sklrn.linear_model.Lasso(alpha=1.0, ‥‥)
sklrn.linear_model.Ridge(alpha=1.0, ‥‥)
sklrn.linear_model.ElasticNet(alpha=1.0,‥‥)
正則化の実施例として、ライブラリに実装されている3類型で十分だと思いますが、念のため、残りの四規演算の可能性についても言及しておきましょう。
別の可能性(加算以外)
第1に、減算の可能性について検討します。ここでは、正則化項の符号を正から負に変えることができるか否かが論点になります。 結論としては減算する意味がないと考えます。その理由は、損失項を減少させる符号の向きと、正則化項を減少させる符号の向きを一致させる必要があり、正則化項の符号向きを反転させてしまうと正則化の機能が失われるからです。あと、λ1,λ2の正負も一緒に反転することで、実質的には加算の場合と等価になります。
第2に、乗算・除算について検討します。ここでは、(損失項)×(正則化項)あるいは(損失項)÷(正則化項)のような表現ができるか否かが論点になります。
例えば、∑|W|の項を乗算しようとすると、ノルム=0の場合が最適解となってしまい、目論見通りの結果が得られません。同様に、∑|W|の項を除算しようとすると、ノルム=∞の場合が最適解となってしまい、やはり目論見通りの結果が得られません。そこで、以下のように工夫することで、正則化の意味をなす目的関数が得られます。F,L,λ1,λ2は上記で説明した通りであり、Aは正値のハイパーパラメータです。
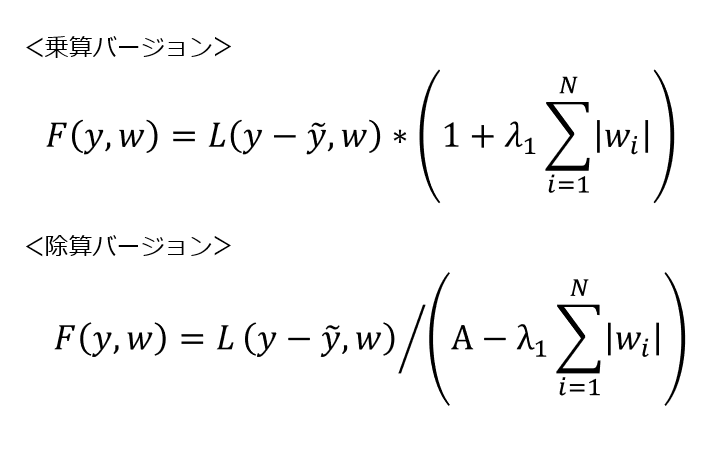
【数式2】乗算・除算を伴う目的関数の試作例
これらの試作関数はいずれも微分可能であるため一応演算可能ですが、実際に、正則化の機能を果たすのかどうかは一目で解りません。あと、目的関数の形状がより複雑になれば勾配降下法の微分演算に時間が掛かってしまうという別の問題も生じ得ます。このような実施例を採用するか否かについての判断に迷いますが、一応、AI弁理士の立場から「採用」の方向で進めましょう。
以上、今回(第2回)は、正則化の実施例について、よく知られる3つの類型を挙げて説明し、他の可能性についても検討しました。次回(第3回)は、過去2回分の検討結果を踏まえ、クレーム骨子を作成してみます。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。











ディスカッション
コメント一覧
まだ、コメントがありません