正則化(1/4)発明の概要
はぐれ弁理士 PA Tora-O です。今回のテーマとして、ディープラーニングで頻出の正則化を題材に取り上げていきます。
背景
ディープラーニング(DL)では、結合重みやバイアスなどの学習パラメータを逐次的に更新することで学習が行われます。畳み込みニューラルネットワーク(CNN;Convolutional Neural Network)の登場以来、演算ユニットの個数をより多く、ネットワークの階層をより深く、という設計思想が主流になりました。例えば、Alexnet(Krizhevsky et al.の論文を参照)では、2012年当時であっても既に60,000,000(六千万)個もの学習パラメータが使われていたようです!
問題の所在
このように、ネットワーク規模が無尽蔵に大きくなるようなアーキテクチャ設計ができるため、学習パラメータの自由度が高くなり過ぎて最適解が一意に定まらない状況が起こります。これを模式的に表現すると、図1のグラフ(学習パラメータ vs 目的関数)のようになります。簡単のために1個の学習パラメータに着目していますが、要は、損失項(=学習誤差)が、無数の大局的最小点(Global Minima)を有する形状になることを意味します。
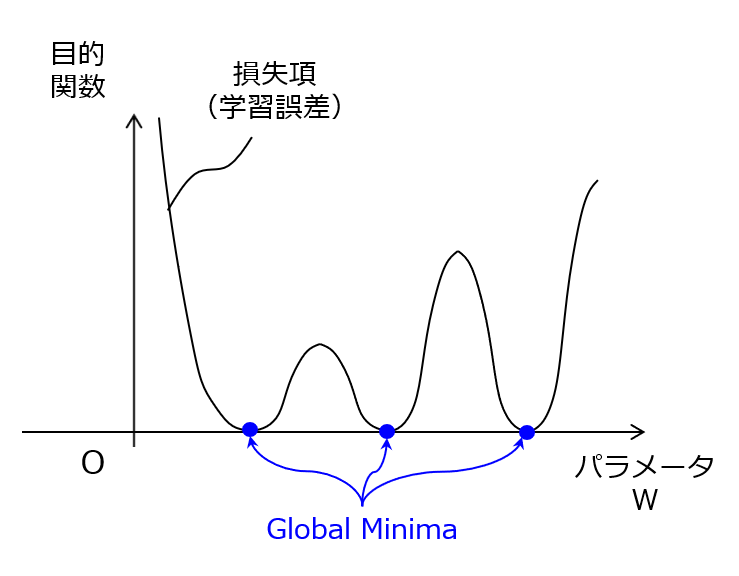
【図1】損失項(=学習誤差)の形状的特徴
例えば、無数にあるうちの1つの収束解が偶然にも汎化性が高ければ何も問題がないのですが、通常は、訓練データに対して過度に適合した収束解に到達し、いわゆる過学習(overfitting)の状態に陥ってしまいます。これに対して、教師データの個数を増やして過学習を抑制するのが望ましいですが、現実的には難しい状況が多いと思われます。
ちなみに、スタンフォード大学のBernard Widrow教授によれば、学習パラメータの総数の10倍以上の教師データが必要であるとのことです。これが、日本ディープラーニング協会(JDLA)G検定でしか聞いたことがないバーニーおじさんのルールです(謎)。
解決手段
そこで、上記した問題を解決すべく、正則化(Regularization)という技術が提案されました。端的に言えば、正則化は、「損失項に対して、スパース化を促進させる正則化項を加算する」ことに特徴があります。ここで、スパース化とは、学習パラメータセットのうち値が0に近くなるようなパラメータ数をなるべく増やす方策を意味し、学習パラメータセットの次元削減(dimension/dimensionality reduction)に近い概念です。
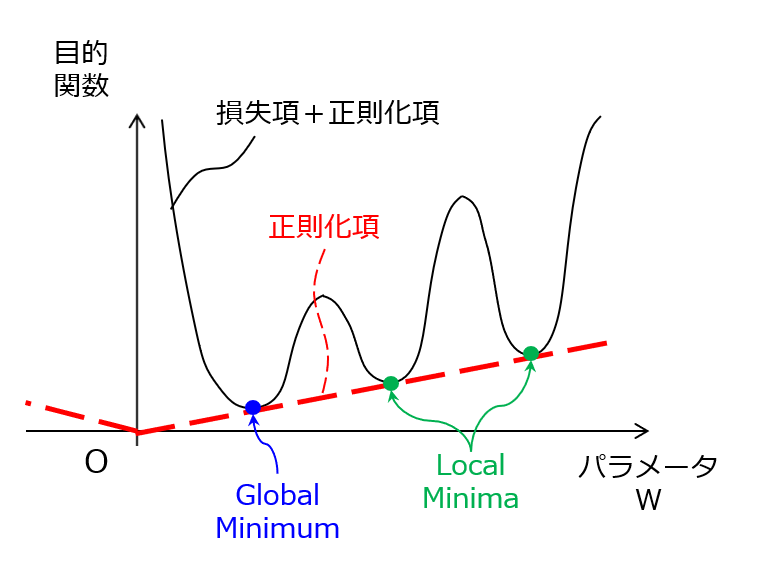
【図2】正則化のメカニズム
図2に示すように、図1の損失項に対して、|W|が増加するにつれて値が大きくなる正則化項を加算することで、損失項がいずれも同値であった複数の大局的最小値に対して、|W|に応じたペナルティが課されます。そうすると、|W|が相対的に大きい側にあった大局的最小点が局所的最小点(Local Minima)に格下げされるので、スパース化された学習パラメータセットが収束解として選択されやすくなります。つまり、正則化項を含む目的関数を用いた学習を通じて、学習パラメータセットの自由度を実質的に下げる効果が生じ、その結果として過学習が起こりにくくなるのです。
ところで、正則化と類似する用語として、正規化(Normalization)と標準化(Standardization)があります。混同しないように注意してください。
- 正規化とは、無次元量化すること。例えば、[0,1]の範囲に収まるように線形変換を行うこと、ベクトルのノルムを1に変換すること、などが挙げられます。
- 標準化とは、平均0、標準偏差1になるように変換すること。
以上、今回(第1回)は、正則化について、その背景を含めて説明しました。この技術を詳しく知りたい方は、例えば、「ニューラルネット」&「正則化」で検索してください。次回(第2回)は、正則化の実施例について検討していきます。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。










ディスカッション
コメント一覧
まだ、コメントがありません