ReLU関数 (3/5) 活性化関数の要求仕様<後半>
はぐれ弁理士 PA Tora-O です。前回(第2回)では、活性化関数の要求仕様について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。
前回検討の補足
第3要件:活性化区間における傾きが1であること。
ところで、この第3要件に関して、単に勾配消失を防ぐのであれば活性化関数の傾きを1に限定する必要はないのでは?と考えた方もいるでしょう。むしろ、傾きを2とか3に設定した方がより好ましいのでは?という意見です。確かに、活性化関数をmax(2x,0)に設定したとき、2倍になった傾きを相殺すべく結合重みを全体的に1/2倍にすれば、傾きが1である場合と等価の学習結果が得られるとも言えそうです。
ところが、関数の傾きがそれぞれ1より大きい場合には、項数の増加につれてプロダクトが増幅するので、今度は勾配爆発(Exploding Gradients)が問題になります。つまり、逆伝播の過程において誤差の勾配が爆発し、入力層付近での学習が進みにくくなります。
このように、状況にもよりますが、基本的には、傾きの値は、何乗しても一定値になる「1」が最も望ましいです。上記した学習結果の等価性と、収束性の良し悪しは別の問題であると言えます。そのあたりを誤解しないように気を付けましょう。
要求仕様のクレーム化
続いて、既に定義した3つの要件を使ってクレーム骨子を作成してみます。ここでは、勾配消失/勾配爆発を抑制することを課題に挙げて検討してみます。まずは、活性化関数が満たすべき要件を3つ挙げます(再掲)。
- 第1要件:連続関数であって広義単調増加であること。
- 第2要件:全区間線形性が破れていること。
- 第3要件:活性化区間における傾きが1であること。
第1要件は、活性化関数にとって重要な事項ですが、勾配消失/勾配爆発との関連性が低いと思われます。クレームの構成から除外しても特に問題なさそうです。
第2要件は、「全区間線形性の破れ」がちょっと何言ってるか解りません。クレームへの適用にあたって表現の見直しが必要ですが、第3要件の検討を先に済ませましょう。
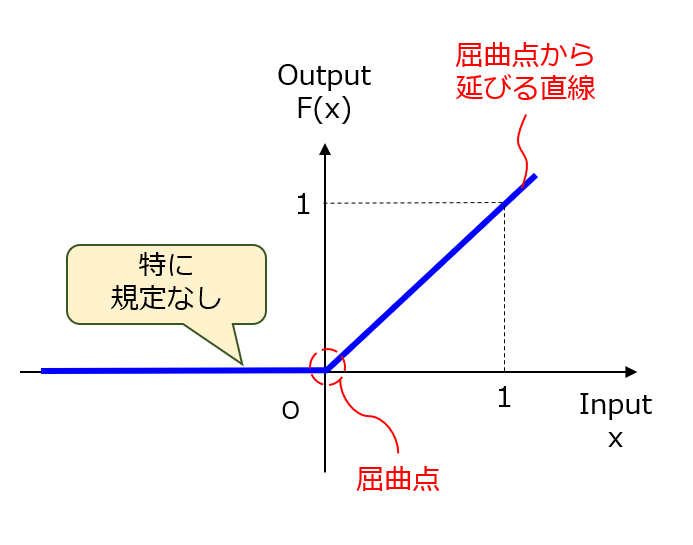
第3要件は、「活性化区間」という表現がやや不明確です。そこで、「区間」の文言を用いずに曲線の形状のみで表現してみます。例えば、ある点(x=0)から正側に延びる直線の勾配が1である、というイメージでしょうか。ReLU関数の場合、「ある点」とは屈曲点に相当するので、この表現を使ってしまいます。なお、屈曲点は基本的にはx=0ですが、活性化関数にバイアス(閾値)が含まれると解釈した場合にはx≠0になり得ます。したがって、屈曲点の座標をx=0に特定しない方が良さそうです。
第2要件に戻って、前回で説明した通り、屈曲点の存在を示すことで全区間線形性の破れがあることを暗に表現できているため、「全区間線形性の破れ」の文言を使わずに済みました。
それでは、改めて作成し直したクレーム骨子は、以下の通りです。
【クレーム骨子】(第2形態)
複数の演算ユニットを含んで構成されるニューラルネットワークを用いた演算方法であって、少なくとも1個の演算ユニットの活性化関数が、以下の2つの条件A,Bを同時に満たすことを特徴とする演算方法。
(条件A)全区間内に少なくとも1つの屈曲点があること。
(条件B)屈曲点から正側に延びる直線の傾きが1であること。
以上、今回(第3回)は、活性化関数の要求仕様について補足的に説明し、改めてクレーム骨子を作成しました。次回(第4回)は、ReLU関数の改良案を紹介しつつ、クレーム第2形態の妥当性を評価してみます。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。








ディスカッション
コメント一覧
まだ、コメントがありません