Word2Vec(3/4)Skip-gramモデル
はぐれ弁理士 PA Tora-O です。前回(第2回)では、CBOWモデルの概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回(第3回)は、Word2Vec を構成するもう一方の ”Skip-gram” モデルの概要について一通り説明してみます。予想通りこのモデルはCBOWに近いため、前回の記事を読んだ方は、さっと流し読みできる内容になっています。
問題の設定
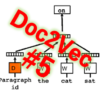
”Skip-gram” では、図1に示す穴埋め問題について取り組みます。以下の説明では、「ゼロから作るDeep Learning(2) 自然言語処理編」(オライリー・ジャパン発行)の例を参考にさせて頂きます。

実際の試験問題では紙面スペースなどの都合から選択肢が狭まっていますが、ここでは、データベースに登録されているすべての単語(N個)の中から1個ずつ選択され得ることにします。
学習モデル
続いて、上記した穴埋め問題を解くための学習モデルを図2に示します。
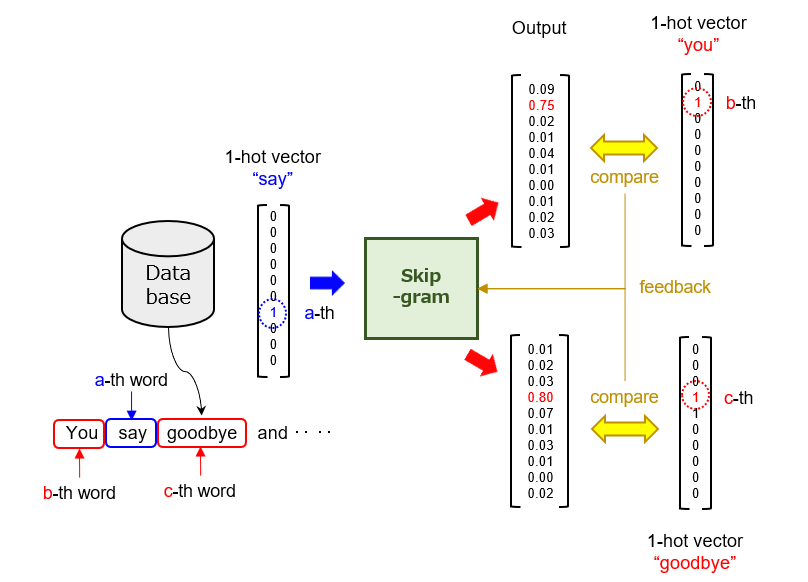
教師データは、データベースに蓄積された複数の文章から生成されます。穴埋め問題の例では、入力値が(say)に相当し、出力値が(you/goodbye)に相当します。これらの単語は、0/1の離散値(Discrete Values)からなる直交基底ベクトル(いわゆる、“1-hot vector”)によって表現されます。この “1-hot vector” は、BoW(Bag-of-Words)の特殊形とも言えます。
そして、ターゲットの単語を示すベクトルを入力した「Skip-gram」は、[0,1]の連続値(Continuous Values)からなる2組のベクトルを出力します。一方のベクトルは「先出単語」の確度(スコア)分布に相当し、他方のベクトルは「後出単語」の確度(スコア)分布に相当します。あとは、通常の「教師あり学習」の場合と同様に、損失関数の計算と学習パラメータの更新を行います。
ネットワーク構造
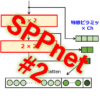
続いて、“Skip-gram” モデルのネットワーク構造を図3に示します。
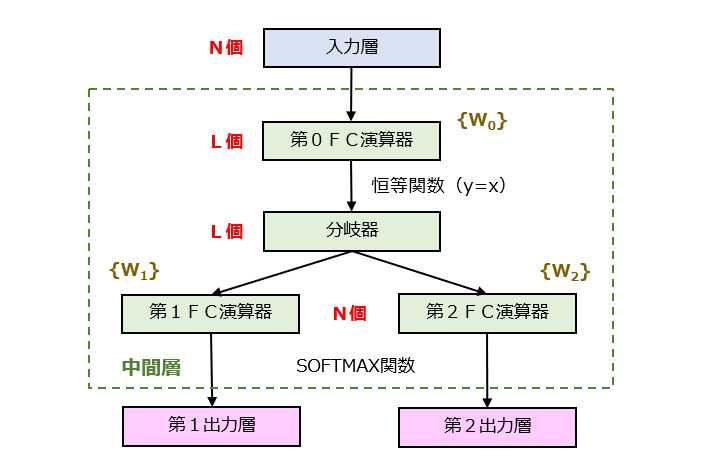
入力層のユニット数を「N」、中間層の入力側ユニット数を「L」とするとき、N>Lの関係を満たすように設計されています。つまり、中間層においてベクトルの次元数を削減する次元削減(Dimensionality Reduction)が行われる点に留意しましょう。ちなみに、分岐器は、第0FC(Fully-Connected)演算器からのL個の出力値を複製した後、第1,第2FC演算器に向けてそれぞれ出力します。
なお、上記した学習モデルでは、正解が1個のみである前提で説明していますが、2個以上の正解があってもOKと思われます。直感的には、出力側の活性化関数をソフトマックスからシグモイドに変更することで実現できそうです。前回では触れなかったCBOWモデルについても同様です。
ベクトル表現の獲得
このように構築された “Skip-gram” モデルを用いて、上記した穴埋め問題を解くことができます。これはこれで有用なのですが、本来の目的は、各々の単語を定量的に表現すること(いわゆる、ベクトル表現の獲得)にあります。
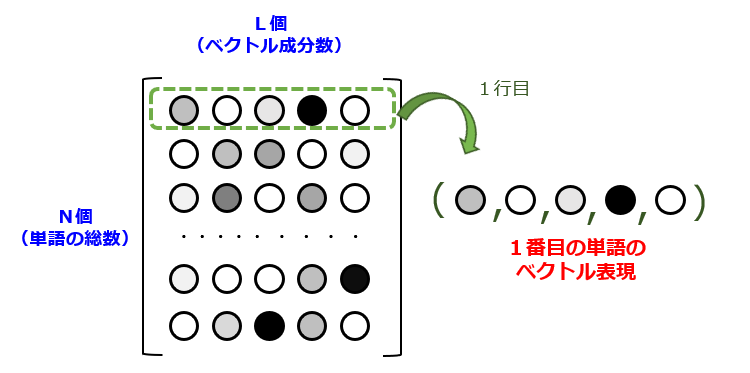
図4に示すように、学習を通じて計算された結合重みのセット(N×L行列)のうち、任意の行を抜き取ることで、各々の単語に対応するL次元ベクトルを求めることができます。つまり、結合重みの大きさが単語間の関連性の高さに相関することを意味します。ここで、N次元ベクトル(one-hot vector)の各成分が「単語の有無」を示すのに対して、L次元ベクトルは人間にとって解読不能な特徴量(機械学習を通じて自動的に設計された特徴量)の集合である点に留意しましょう。なお、結合重み行列は、{W0},{W1},{W2}のうちのいずれの行列を使っても大差ありません。
以上、今回(第3回)は、“Skip-gram” モデルについて、CBOWモデルと同様の流れに沿って説明しました。テーマ最終回(第4回)では、何か適当にクレームを作って総括したいと思います。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。







ディスカッション
コメント一覧
まだ、コメントがありません