ReLU関数 (5/5) 総括
はぐれ弁理士 PA Tora-O です。前回(第4回)では、ReLU関数の改良策を色々紹介しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。
前回のレビュー結果を踏まえ、最終的に、次のような発明ストーリーを作成してみました。仕事ではないのでやや雑に書きますがご了承ください。
発明ストーリー
【従来技術】
複数の演算ユニットから構成される階層型ニューラルネットワークにおいて、演算ユニットの入出力特性を示す活性化関数として、一般的には、シグモイド関数やtanh関数などの非線形関数が用いられる。
【問題点と課題】
問題点は、学習パラメータセットを更新する際に、誤差逆伝播法に起因する更新量の減衰または増幅が起こり、学習不足などによって推論精度が低下すること。
課題は、階層型ニューラルネットワークの推論精度を向上すること。
【クレーム】(最終形態)
複数の演算ユニットを含んで構成される階層型ニューラルネットワークを用いた演算方法であって、少なくとも1個の演算ユニットの活性化関数が、以下の2つの条件A,Bを同時に満たすことを特徴とする演算方法。
(条件A)全区間のうち屈曲または湾曲する少なくとも1つの変曲点があること。
(条件B)変曲点から正側に延びる直線または線分の傾きが1であること。(169文字)
【作用と効果】
演算規則を定める学習パラメータセットの更新量を誤差逆伝播法に従って決定する際に、演算ユニットの活性化関数が有する変曲点から正側に延びる直線または線分の傾きを1にすることで、少なくとも傾きが1である区間では当該傾きの乗算に起因する学習誤差の勾配の減衰または増幅が起こらない。つまり、階層型ニューラルネットワーク内の逆伝播方向への逐次的更新が促進され、その分だけ学習不足が解消されやすくなる。その結果、階層型ニューラルネットワークの推論精度が向上する。
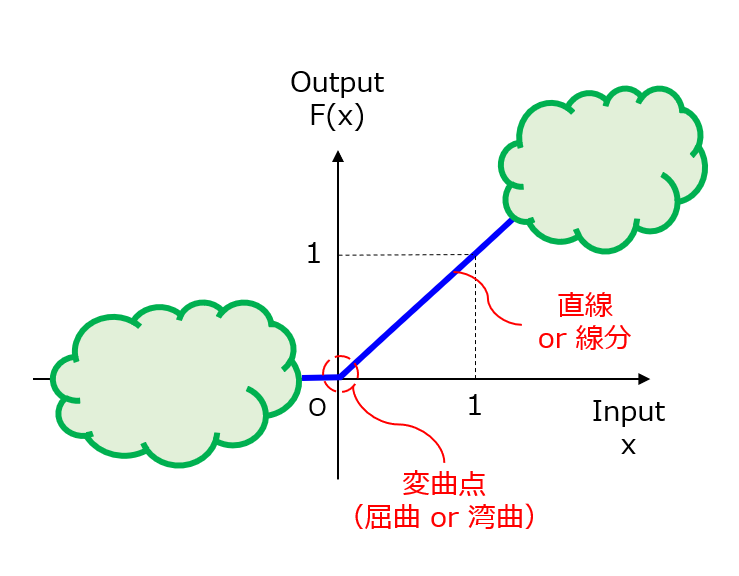
【図】活性化関数とクレーム構成の間の対応関係
作者コメント
1.クレーム
ニューラルネットワークに演算方向があって誤差逆伝播法が適用できることを明示するため、「階層型」を追加しました。また、ELU(前回参照)をクレーム範囲に含めるため、「屈曲または湾曲」と並列的に記載しました。さらに、ReLU6(前回参照)をクレーム範囲に含めるため、「直線または線分」と並列的に記載しました。
ところで、権利侵害者の製品に学習済みモデルのみが実装されている場合、権利者自身が当該製品を解析することによって、誤差逆伝播法を用いて学習パラメータセットが決定された事実を立証するのは実質的に不可能であると思われます。そのため、今回のクレーム構成では、侵害検出性を高めるべく、誤差逆伝播法を用いるという特徴が意図的に除外されています。
2.課題と効果
ReLU関数によって解決される課題は、学習フェーズの実行中に勾配消失/爆発を抑制することです。これには特に異論はありません。ところが、最終形態クレームでは、学習フェーズというよりもむしろ推論フェーズを想定している表現になっており、上記した課題をそのまま使いにくい状況になっています。そこで、勾配消失/爆発に起因して下流側で発生する事象、すなわち学習不足ひいては推論精度の低下を問題点として挙げるような発明ストーリーに変更しています。展開がちょっと強引であることは否定しませんが、致し方がないところでしょう。
3.まとめ
今回の検討の流れでは、シグモイド関数やtanh関数のみが公知であり、ReLUや派生関数が公知でないことを仮定したので、後知恵も駆使しながら概ね最強の包括クレーム(Generic Claim)を作ることができました。このクレームであってもカバーできない他の派生関数が存在すると思われますが、自身の知識不足ということでご容赦ください。
ところで、非公知であると仮定した派生関数のうち1つでも既に公知であった場合、どうなるでしょうか。当然ながら現在のクレームを限縮する補正を行わなければならず、しかも権利化が格段に難しくなりそうです。そこで、出願を検討する際に、発明を多面的に捉えて様々なクレームの作成を試みる、というのが実務上の最善策になりそうです。具体的には、関数形状の具体化に拘らず、ネットワーク構造の具体化(例えば、入力側に近い演算ユニットに適用する点)など様々な観点で検討できるはずです。
以上をもちまして、ReLUを含む活性化関数の事例検討を終了します。次回から、また別のテーマに移ります。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。











ディスカッション
コメント一覧
まだ、コメントがありません