Unrolled GAN(4/4)総括
はぐれ弁理士 PA Tora-O です。前回(第3回)では、Unrolled GAN の学習メカニズムについて概説しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回(第4回)は、クレームを含む発明ストーリーを作成し、これまで3回分の検討を総括します。
発明ストーリー
【従来技術】
代表的な生成モデルとして、データの真贋判定を行う弁別器(Discriminator)と協働して生成器(Generator)を学習させる敵対的生成ネットワーク(GAN)が知られている。
【問題点と課題】
問題点は、GANの学習途中で、目的関数の局所的極小点(Local Minima)に嵌まり込みやすく、学習に時間が掛かってしまうこと。
課題は、GANの学習時間を短縮すること。
【クレーム骨子】(Unrolled GAN)
弁別器の演算規則を特定可能な第1学習パラメータ群を第1引数とし、生成器の演算規則を特定可能な第2学習パラメータ群を第2引数とした敵対的損失項を含む目的関数に従って、勾配降下法を用いて敵対的生成ネットワークを学習する方法であって、
第2学習パラメータ群が固定された目的関数に従って第1学習パラメータ群を予備的に更新する回数を第1更新回数、かつ
第1学習パラメータ群が固定された目的関数に従って第2学習パラメータ群を予備的に更新する回数を第2更新回数、と定義するとき、
第1学習パラメータ群の本更新に用いられる目的関数の第1引数における第1更新回数が、第2学習パラメータ群の本更新に用いられる目的関数の第1引数における第1更新回数と異なり、または、
第1学習パラメータ群の本更新に用いられる目的関数の第2引数における第2更新回数が、第2学習パラメータ群の本更新に用いられる目的関数の第2引数における第2更新回数と異なることを特徴とする学習方法。(416文字)
【作用効果】
弁別器および生成器が同様の進行度合いで学習を繰り返す過程において一時的に、両者の間で相互依存性の過学習が発生し、目的関数の局所的極小点に嵌まり込むことがある。そこで、関数形状が共通する目的関数において、本更新に先立って学習パラメータ群を予備的に更新するとともに、本更新に用いられる第1または第2引数における更新回数に差を設けることで、勾配降下法に基づいて目的関数の大局的最小点(Global Minimum)に到達するまでの間は、第1および第2学習パラメータ群の更新に関する独立性を高めることができる。
そうすると、弁別器と生成器の間で起こり得る相互依存性の過学習が抑制され、目的関数の局所的極小点に嵌まり込んで学習が停滞する可能性が低下する。これにより、敵対的生成ネットワークにおける学習時間を短縮することができる。
作者コメント
上記したクレームと、実施例(Unrolled GAN)の関係について補足的に説明します。
まず、弁別器Dの「第1」更新回数をN(≧0)とし、生成器Gの「第2」更新回数をM(≧0)とします。次の図で、目的関数の引数ペアを(N,M)と表現し、グラフにプロットしてみます。
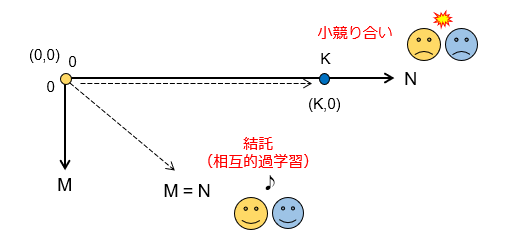
Unrolled GAN では、弁別器Dが(0,0)に、生成器Gが(K,0)にそれぞれ対応します。M=Nの45度ラインが通常の更新則(つまり、D-G結託線)に該当しますので、Unrolled GAN は、このラインからベクトル向きが最も離れており、しかも2点のプロットが効率的に離された最適パターンになっています。つまり、相互依存性の過学習を抑制するという観点では、Unrolled GAN がまさにベストモードと言えるでしょう。
一方、上記した考え方に従うと、N,Mの値を反対にした(0,K)も同様であるとも主張できます。ところが、一般的に言えば、生成器Gは、弁別器Dよりも保有するパラメータ数が多く、その分だけ学習の収束性が低くなるはずです。そのため、実際には、逆効果であるとまでは言い切れないが、Unrolling による効果が薄まるのでは、と勝手に予想します(未検証)。
以上をもちまして、Unrolled GAN の事例検討を終了します。次回から、また別のテーマに移ります。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。








ディスカッション
コメント一覧
まだ、コメントがありません