VAE(1/4)オートエンコーダの概要
はぐれ弁理士 PA Tora-O です。今回のテーマとして、深層生成モデルの基礎とも言うべきVAE(Variational Autoencoder)を題材に取り上げていきます。
背景
生成モデル(Generative Model)とは、所与の学習データセットをベースに、学習データとは異なる新しいデータを人工的に生成するためのモデルです。データの種類は、静止画、動画、音声(楽曲、音、声など)、文章(小説、俳句、チャットなど)など多岐にわたりますが、以下、画像(静止画)を例に挙げて説明していきます。画像は、多値(8ビットの場合は、256通り)の中から選択し得る画素値を有する多数の画素(例えば、100×100画素)からなるデータであり、場合によっては複数のカラーチャンネル(RGB)をもっています。つまり、画像領域の全体的または局所的なバランスを考慮しつつ、より自然な状態で違和感なく仕上げる必要があることから、「画像生成」はかなり難度が高いタスクであると言えます。
従来では、マルコフ連鎖モンテカルロ法(MCMC法)などを含む統計的手法が主流でしたが、画像を完成させるまでの演算時間が掛かるという問題がありました。そこで、学習フェーズには演算時間が掛かるものの、生成フェーズには演算時間がそれほど掛からないニューラルネットワークを用いた新しい手法が出現しました。ニューラルネットワーク系の生成モデルは、
[1]VAE(Variational Autoencoder)
[2]GAN(Generative Adversarial Network)
の2種類に大別されます。今回は、前者のVAEについて事例検討を進めますが、その前に、ネットワーク構造のベースとなるオートエンコーダ(AE)について軽く触れておきます。
オートエンコーダの概要
オートエンコーダは、ニューラルネットワークを用いた特徴量抽出手法の一種であり、日本語では「自己符号化器」と呼ばれています。ネットワーク構造の一例を次の図に示しています。
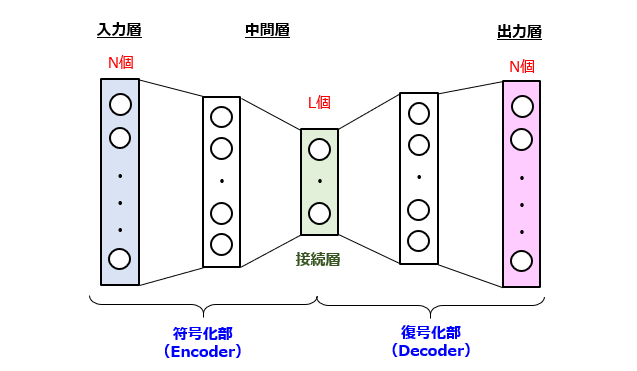
オートエンコーダは、基本的には、入力層と、1層以上の中間層と、出力層から構成されます。演算ユニットの個数に関して、ざっくり次の2つの特徴があります。
・入力層と出力層の間で個数(=N)が等しいこと
・特定の中間層(接続層)に関して、N>Lを満たすこと
この形状的特徴から、オートエンコーダは、以前には、砂時計型ニューラルネットワークとも呼ばれていたようです。このネットワークでは、入力層に入力されるN次元データと、出力層から出力されるN次元データが一致するように学習を行います。この学習(いわゆる、教師なし学習)を通じて、学習データセットの潜在的特徴(Latent Features)を獲得することができます。
この潜在的特徴は、砂時計のくびれ(オリフィス)に位置する接続層が出力するL次元のベクトルに相当します。つまり、オートエンコーダの前段はデータをN次元→L次元に圧縮する符号化部(Encoder)に、その後段はデータをL次元→N次元に復元する復号化部(Decoder)にそれぞれ対応します。
上の図では、入力/出力データがフラット化された1次元ベクトルとして表現していますが、画素が2次元的に配置された画像にも適用できます。この場合、中間層は、畳み込みニューラルネットワーク(CNN;Convolutional Neural Network)を構成する各層や、逆畳み込みニューラルネットワーク(DNN;Deconvolutional Neural Network)を構成する各層からなります。
具体的に、CNNの場合には、畳み込み層、プーリング層、全結合層、正則化層が含まれます。一方、DNNの場合には、逆畳み込み層、アンプーリング層、全結合層、正則化層が含まれます。なお、CNNを構成する各層の機能については、過去の記事を参考にしてください。
参考:全体平均プーリング(1/5)背景技術
ちなみに、このオートエンコーダは、一般的には、外れ値(Outlier)の検出や、データのノイズ除去(Noise Reduction)などに用いられるのですが、VAEではこれとは違う使い方をします。
以上、今回(第1回)は、VAEの背景やオートエンコーダの概要について説明しました。次回(第2回)は、VAEの実施例について説明します。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。









ディスカッション
コメント一覧
まだ、コメントがありません