VAE(3/4)理論的な裏付け
はぐれ弁理士 PA Tora-O です。前回(第2回)では、VAEの実施例について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回(第3回)は、VAEの理論的な裏付けについて説明します。
数学的解釈
前回では、学習フェーズにおいて、エンコーダが z=μ+σ・ε の演算を行った後、得られたL次元特徴ベクトル{z}をデコーダ側に出力する旨を説明しました。ここで、ε は、標準正規分布に従って生成される標本値です。つまり、仮に同一の学習データ(ここでは、画像)を入力した場合であっても、標本値 ε が変動することで、その都度異なる特徴ベクトルが出力されると理解できます。ここが、従来型のオートエンコーダと異なる点です。VAEの数学的解釈について、次の図1を参照しながら説明します。
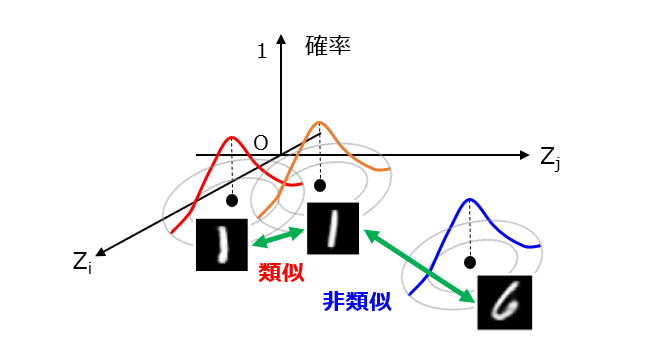
この図1は、各々の画像と特徴ベクトルの間の対応マップを示しています。実際には、(L+1)次元空間ですが、絵心がないのでL=2として作図しています。例えば、類似度が高いほど互いに近くなるように画像が配置される一方、類似度が低いほど互いに遠くなるように画像が配置されます。ここまでは、一般的な埋め込み(Embedding)の話と全く同じです。しかし、VAEでは、個々の画像の特徴を「点」ではなく「拡がり」と捉えて、潜在的空間上の確率分布を与えている点が重要です。
実現方法
それでは、VAEの学習パラメータが上記した数学的意味を獲得するためには、何をどのように設計すればよいでしょうか? その答えは、目的関数にあります。VAEの学習に適した目的関数の一例を図2に示します。
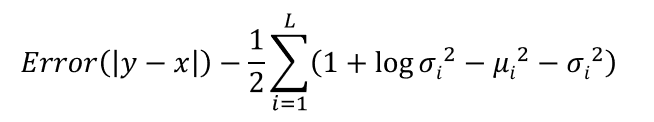
第1項は、入力-出力画像の類似度を評価するための指標(誤差項あるいは損失項)であり、例えば、RMSE(Root Mean Square Error)、MAE(Mean Absolute Error)などが挙げられます。ここでは、第1項=0が理想状態であるとしましょう。
第2項は、画像の埋め込み位置に制約を課すための正則化項であり、カルバック・ライブラー情報量(Kullback–Leibler divergence)に相当します。この第2項を導入することで、[1]ピーク位置(μ)を原点O中心に密集させ、かつ[2]標準偏差(σ)の大きさを1に寄せるような作用が働きます。
画像の生成結果
このようにして学習フェーズが終了した後、VAEのデコーダ部分のみを用いて、様々な画像を生成することができます。図3は、L=2として、生成済みの画像(顔と数字)を2次元マップ化したものです。

出展:Tutorial on Variational Autoencoders
このように、学習データセットに含まれない画像も、より自然な状態で仕上がっています。その理由は、デコーダの学習過程で確率分布を導入した為と考えられます。つまり、学習データセットを構成する個々の学習データのみならず、その学習データ同士の中間状態を確率論的に表現することで、複数の学習データを尤もらしくアレンジして新たなデータを創作する能力をデコーダに学習させることができます。公知の構成同士を組み合わせて進歩性のある発明(invention)を生み出す、何となく特許(patent)に通じるものがあります。
以上、今回(第3回)は、VAEの理論的な裏付けについて説明しました。テーマ最終回(第4回)は、過去3回分の総括として、一連の発明ストーリーを作成します。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。










ディスカッション
コメント一覧
まだ、コメントがありません