CycleGAN（2/4）実施例の説明
はぐれ弁理士 PA Tora-O です。前回（第１回）では、CycleGAN の概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回（第２回）は、CycleGAN の実施例について説明します。
システム構成
まず、システム構成について、図１を参照しながら説明します。
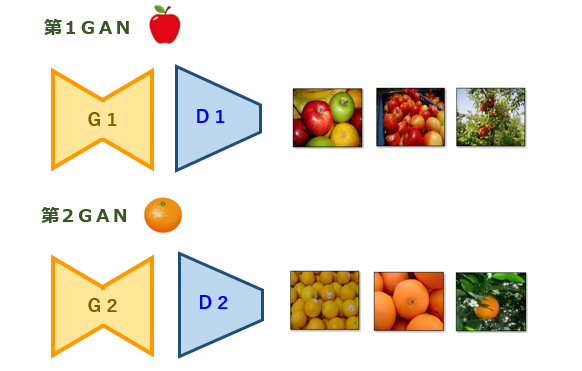
CycleGAN は、２系統のＧＡＮで構成されます。一方の第１ＧＡＮは、オレンジ（Orange）からリンゴ（Apple）への画風変換を行うネットワークです。他方の第２ＧＡＮは、リンゴからオレンジへの画風変換を行うネットワークです。学習用画像として、リンゴを共通の特徴とする画像の集合体である第１画像群、オレンジを共通の特徴とする画像の集合体である第２画像群、の２つのグループを準備します。図１から理解されるように、第１画像群と第２画像群はそれぞれ独立して準備されたものであり、オブジェクト（ここでは、果物）のサイズ・個数・配置などを両方の画像間で揃える必要がない点に注目です。
Adversarial Loss
続いて、目的関数（Objectives）の第１要素である敵対的損失（Adversarial Loss）について、図２および図３を参照しながら説明します。
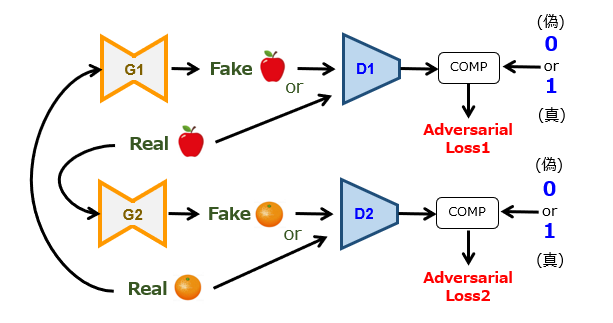
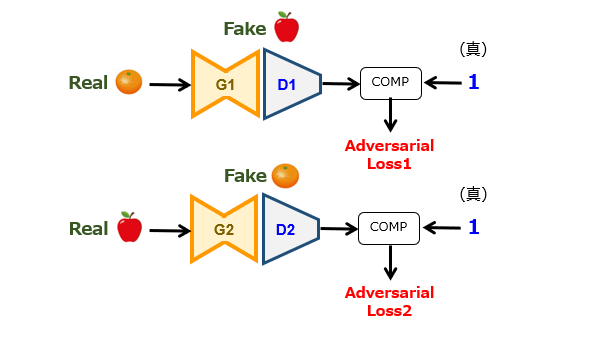
損失項の計算方法は、基本的には、Pix2Pix の場合と同じです。ただ、ＧＡＮが２系統あるので、第１，第２生成器に入力される画像群が互い違いになっている点が特徴的です。本図では、出力値が１つですが、PatchGAN を導入してＮ×Ｎ個にしても構いません。
Reconstruction Loss
続いて、目的関数の第２要素である再構成損失（Reconstruction Loss）について、図４を参照しながら説明します。
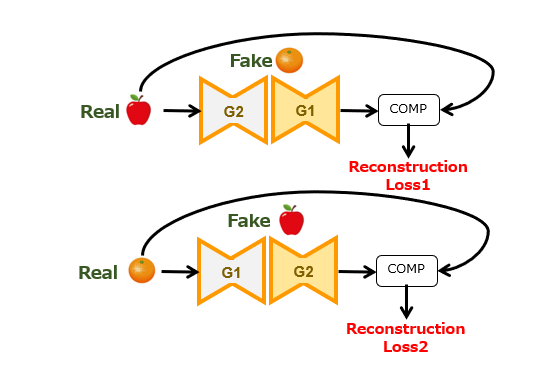
本論文中では、“Cycle-Consistency Loss“ と呼ばれる損失項であり、CycleGAN の命名の由来にもなった概念です。なお、一般的には、再構成損失の方が多用されているようですので、以下、こちらの用語を使って説明します。
再構成損失は、具体的には、
［１］リンゴ画像を生成器Ｇ２，Ｇ１に順次投入すると、元のリンゴ画像が得られること（Forward Cycle-Consistency）
［２］オレンジ画像を生成器Ｇ１，Ｇ２に順次投入すると、元のオレンジ画像が得られること（Backward Cycle-Consistency）
の２つの制約を課しています。つまり、この損失項のペアは、２つの生成器Ｇ１，Ｇ２による変換処理の可逆性を担保するための仕組みといえます。それでは何故、この可逆性を担保する必要があるのでしょうか？ どうやら、これが CycleGAN の核心部分であるように思われます。
以上、今回（第２回）は、CycleGAN の実施例について説明しました。次回（第３回）は、学習のメカニズムについて概略的に解説します。
↓ブログランキングに参加しています。よろしければ１クリックお願いします。
