Selective Search(3/4)発明の概要Ⅲ
はぐれ弁理士 PA Tora-O です。今回(第3回)も引き続き、”Selective Search” の実施例について詳しく説明します。なお、前回(第2回)の復習を行う際は、こちらのリンクからお願いします。
前回は、フローチャートのステップS4まで説明しました。類似度に基づいて階層的グループ化を行ったところです。ここまで説明した間、残念ながら、本発明に特有の特徴事項はなかったような気がします。
S5:境界ボックスの選定
ステップS5では、ステップS4で階層的にグループ化された領域に対して、それぞれ外接する矩形状の境界ボックスを設定します。例えば、初期領域がN個である場合、理論上は、全部で Σk=N・(N+1)/2 個の境界ボックスを設定することができます。ところが、Nの値が大きくなるにつれて、境界ボックスの総数が2乗のオーダーで急増するので、演算高速化の観点で言えばあまり好ましくありません。そこで、”Selective Search” 論文では、次の3つのサブステップを実行することで境界ボックスを選定します。
[5a]序列値Vの算出 V=i・RND
[5b]Vの昇順ソート
[5c]Vが小さい順に境界ボックスを選定
ここで、iは、領域マップの階層を示しており、領域マップを構成する領域数に一致するすインデックスです。また、RNDは、[0,1]の値を取る乱数値です。果たして、序列値V(本論文中では、“positioning value”)を用いた選定によって、どのような効果があるのでしょうか? 以下、図1および図2を参照しながら解説します。
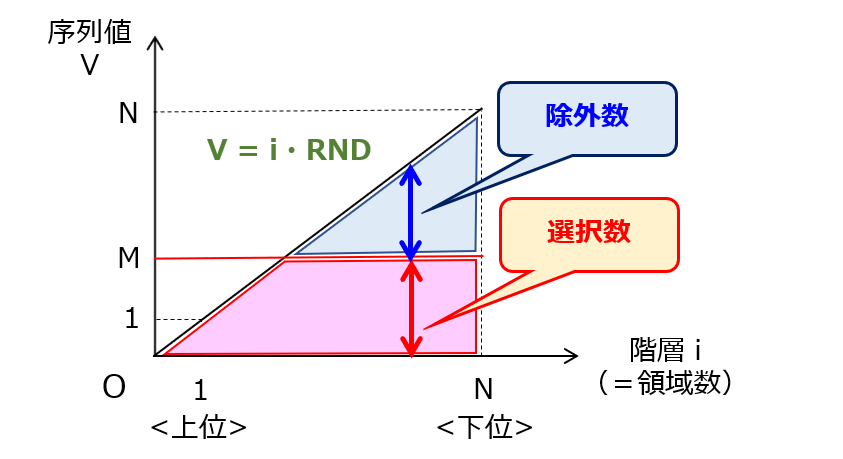
図1に示すグラフの横軸は階層iを、縦軸は序列値Vをそれぞれ示しています。本図において、境界ボックスの選定数を絞ることは、1<M<Nの関係を満たす閾値Mを設定することと等価です。なぜならば、RNDが[0,1]の一様分布に従う値であるからです。この場合、閾値Mは、領域が選択されるべき序列値Ⅴの上限値に相当します。
これにより、閾値Mを用いて、各階層iに対応する領域の選択率を統計的に算出することができます。具体的には、選択数の期待値は A=min(i,M) となり、除外数の期待値は B=i-A=max(i-M,0)となります。選択率の期待値 A/i=min(M/i,1)をグラフ化すると、図2のようになります。
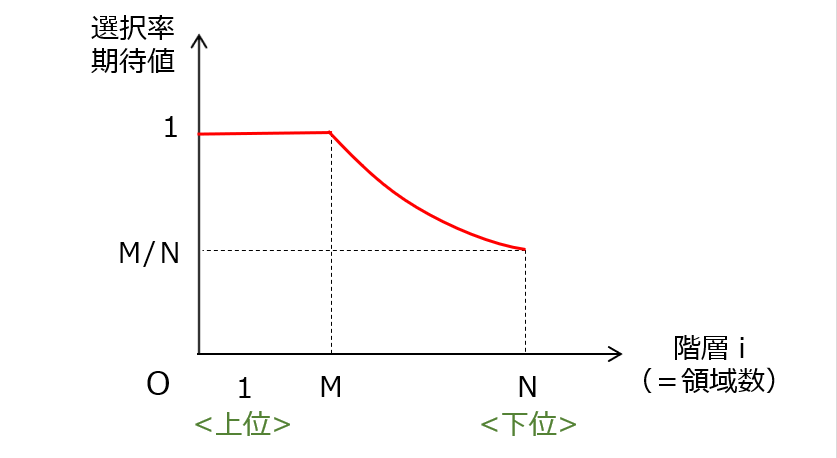
どうやら、図2のグラフそのものが、”Selective Search” の本質を示していそうです。このような重み付けを行うことで何らかの効果が得られるのですが、ここではあえて触れずに次回までの宿題にしておきます。そして、上記した選定を行った結果、図3のように複数の関心領域(ROI)が設定されます。
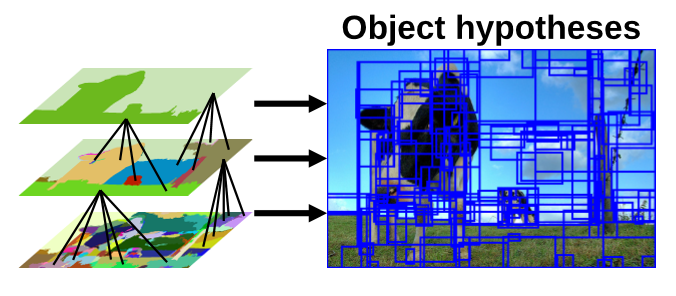
出展:Selective Search for Object Recognition
以上、第1~3回にわたって、”Selective Search” の実施例を説明しました。テーマ最終回(第4回)では、発明ストーリーの作成と本検討の総括を行います。
↓ブログランキングに参加しています。よろしければ1クリックお願いします。










ディスカッション
コメント一覧
まだ、コメントがありません