Unrolled GAN（2/4）実施例の説明
はぐれ弁理士 PA Tora-O です。前回（第１回）では、Unrolled GAN の概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回（第２回）は、Unrolled GAN の実施例について説明します。
Vanilla GAN
まず、元祖ＧＡＮ（Vanilla GAN）の演算式は、以下の図１の通りです。目的関数（敵対的損失：Adversarial Loss）の数式は、過去の事例検討を含めて初出ですが、ここでは主要な変数表記を示すだけに留めておき、詳しい説明を省略します。
Ｄ (・) ：弁別関数（弁別器の処理内容）
Ｇ (・) ：生成関数（生成器の処理内容）
θＤ ：弁別器の学習パラメータ群
θＧ ：生成器の学習パラメータ群
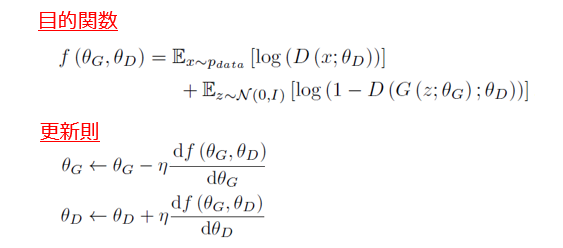
続いて、図２で、学習パラメータ群の更新流れを模式的に示します。
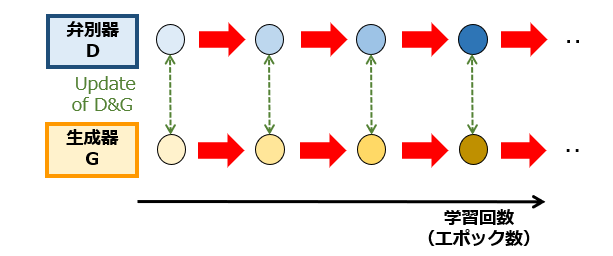
グラフの横軸は、学習回数（あるいは、エポック数）に相当します。丸印（〇）は「学習パラメータ群の状態」を、矢印（➡）は「更新のプロセス」をそれぞれ相当します。つまり、左側にある丸印ほど学習が浅く、右側にある丸印ほど学習が深いことを意味します。
また、上段と下段をつなぐ破線矢印は、目的関数の算出に用いられる学習パラメータ群のペアを示しています。図２から理解されるように、Vanilla GAN では、弁別器および生成器は、学習の各回で予め定められる１つの目的関数に従って更新されます。
Unrolled GAN
一方、Unrolled GAN の演算式は、以下の図３の通りです。
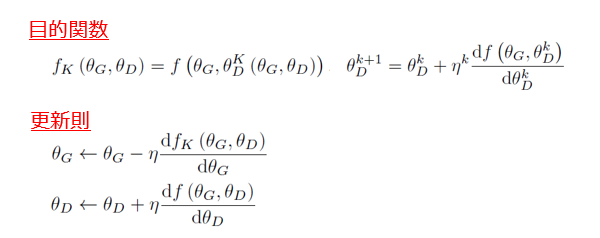
目的関数の形状は、Vanilla GAN（図１）と基本的には同一ですが、２つの引数のうち後者のみが異なっています。弁別器の学習パラメータ群 θＤ は、１回更新されたものと、Ｋ回（Ｋ≧２）更新されたものが使われます。つまり、Unrolled GAN では、弁別器と生成器とは、学習パラメータ群を更新するための目的関数が異なっている点に大きな特徴があります。なお、本論文では、ｋ＝Ｋである目的関数のことを “Surrogate Objective Function”（代理目的関数）と呼んでいます。
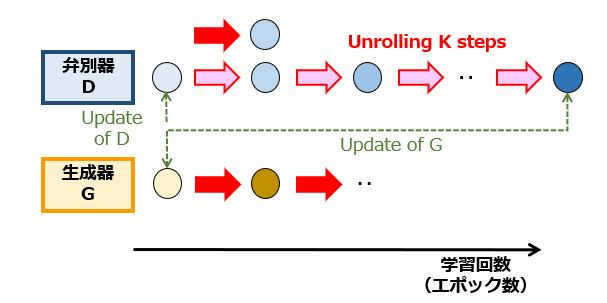
図４は、図２と同様に、学習パラメータ群の更新流れを模式的に示した図です。本論文では、生成器のみをＫ回連続して学習させることを “unroll”（展開する）と呼んでいます。図２と図４を見比べれば、両者の学習方法の違いが明らかです。
以上、今回（第２回）は、Unrolled GAN の実施例について説明しました。このように、Unrolled GAN の特徴事項については理解できるのですが。代理目的関数の導入によってモード崩壊の発生を抑制できる、という技術的根拠を説明するのは大変難しいと思われます。そこで、次回（第３回）は、そのメカニズムについて独自の切り口で概略的に解説します。
↓ブログランキングに参加しています。よろしければ１クリックお願いします。
