Doc2Vec（4/5）ＰＶ－ＤＭ＜前編＞
はぐれ弁理士 PA Tora-O です。第２～第３回にわたって、PV-DBOW モデルの概要について説明しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回（第４回）から、ＰＶ－ＤＭ（Distributed Memory Model of Paragraph Vector）の概要について説明します。
問題の設定
ＰＶ－ＤＭモデルでは、図１に示す穴埋め問題について取り組みます。
これは、Word2vec のＣＢＯＷモデルにおける穴埋め問題と大体同じですが、ヒントとして段落番号が予め提示されている点が異なります。また、PV-DBOW の場合と同様に、データベースに登録されているすべての段落（Ｎ個）を構成するすべての単語（Ｍ個）の中から選択されるとします。
ネットワーク構造
続いて、ＰＶ－ＤＭモデルのネットワーク構造を図２に示します。
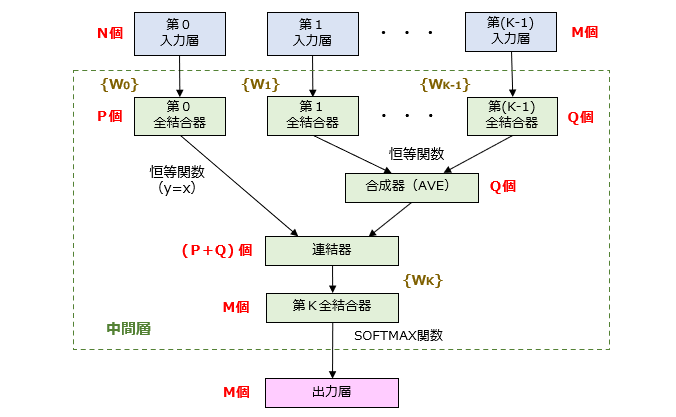
ここで注目すべきは、PV-DBOW モデルにおけるＫ個の出力層が、１層を除き、すべて入力層に振り分けられている点です。そして、段落ＩＤの入力先（第０入力層）が中間層の一部分のみ（Ｐ個のユニット）に接続される一方、単語ＩＤの入力先（第１～第K-1入力層）が中間層の残り部分のみ（Ｑ個のユニット）に接続されることも重要なポイントです。
なお、第１～第K-1入力層のユニット数を「Ｍ」、中間層の入力側ユニット数を「Ｑ」とするとき、Ｍ＞Ｑの関係を満たすように設計されています。なお、Ｐ、Ｑはそれぞれ、次元削減（Dimensionality Reduction）後のベクトル成分数であり、いわゆる設計パラメータに該当するため、これらの大小関係には特に制限がありません。
合成器は、第１～第K-1全結合器から入力された特徴ベクトルの各成分の平均（Average）を求め、得られたＱ個の平均値を連結器に向けて出力します。連結器は、成分数が異なる２つの特徴ベクトルを連結（Concatenate）し、第Ｋ全結合層に向けて出力します。もし、成分数が一致（Ｐ＝Ｑ）する場合、ベクトルの連結に代えて、ベクトルの加算・平均を含む合成処理を行ってもＯＫです。
Paragraph Vector の獲得
このように構築されたＰＶ－ＤＭモデルを用いて、上記した穴埋め問題を解くことができます。しかし、本来の目的は、段落の分散表現（論文で言うところの “Paragraph Vector”）を獲得することにあります。
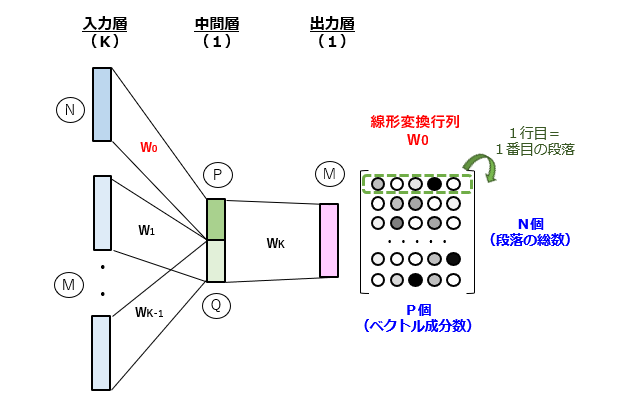
図３に示すように、学習を通じて計算された結合重みのセット、つまり線形変換行列｛Ｗ０｝（Ｎ×Ｐ行列）のうち、任意の行を抜き取ることで、各々の段落に対応するＰ次元ベクトルを求めることができます。このあたりの要領は、PV-DBOW と全く同じです。
以上、今回（第４回）は、ＰＶ－ＤＭモデルの概要について説明しました。ただ、ここまでの説明では、ＰＶ－ＤＭの “Distributed Memory Model” の意図を正しく伝えきれていないと思われます。テーマ最終回（第５回）では、「ＤＭ」に関する補足的な説明を行った後でクレーム骨子の作成を試みます。
↓ブログランキングに参加しています。よろしければ１クリックお願いします。
