RetinaNet（4/4）総括
はぐれ弁理士 PA Tora-O です。前回（第３回）では、フォーカルロスの効果について検討しました。改めて復習されたい方は、こちらのリンクから確認をお願いします。今回（第４回）は、クレームを含む発明ストーリーを作成し、これまで３回分の検討を総括します。
発明ストーリー
【従来技術】
機械学習のための目的関数は、ニューラルネットワークの構成やデータ定義に応じて決定される。一般的には、クラス分類の際には、損失項として交差エントロピー（Cross Entropy）が用いられる。基本的には、１つの検出対象につき、１つのクラスが正解（正例）に、残りすべてのクラスが不正解（負例）に割り当てられる。つまり、クラス分類を行う際に、正例と負例の割合に関する不均衡が生じている。
【問題点と課題】
問題点は、交差エントロピーでは、クラス分類数が増加するにつれて分類精度が低下する傾向がみられること。
課題は、クラス分類数の増加に起因する分類精度の低下を抑制すること。
【クレーム骨子】（RetinaNet）
クラス分類の確率に関する損失項を含む目的関数を用いて学習器を学習する方法であって、
損失項は、交差エントロピーに、確率が高くなるにつれて小さくなる乗数を乗算した関数形状を有することを特徴とする学習方法。（１０８文字）
【作用効果】
確率が高くなるにつれて小さくなる乗数を交差エントロピーに乗算することで、交差エントロピーをそのまま用いる場合と比べて、正例による損失減少への寄与度がより高くなる。つまり、この損失項を含む目的関数を用いて学習を行うことで、クラス分類数が多い場合であっても、正例と負例の割合に関する不均衡による学習精度の低下を防ぐことができる。これにより、クラス分類数の増加に起因する分類精度の低下が抑制される。
作者コメント
フォーカルロスの関数形は、Ｍ（ｐ）・ＣＥ（ｐ）のような関数積で表現されていますが、分離不可能な関数（例えば、ＣＥ[Ｍ(ｐ)] の合成関数）で表現できる可能性もあります。これが気になる場合は、代替案として、「交差エントロピー関数に対する損失項の比が、確率が高くなるにつれて小さくなる」を採用すれば解決しそうです。
ところで、今回の事例検討を行う際に、とある技術を思い出しました。自然言語処理のカテゴリー内で紹介した Negative Sampling です。
事例 #011 Negative Sampling
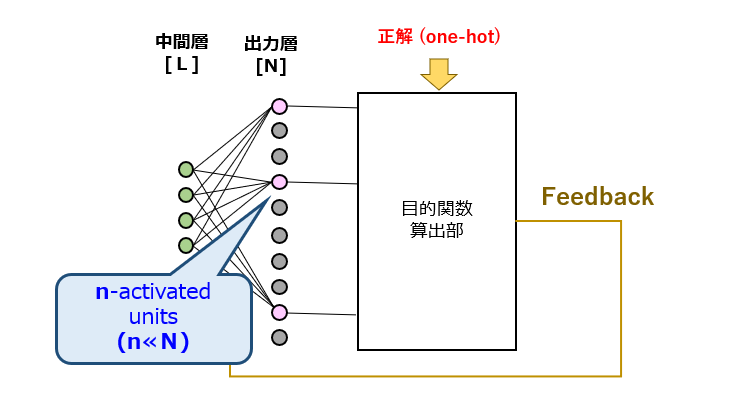
この技術は、一見ドロップアウトに似ていますが、導入目的が異なります。具体的には、コーパスの中から文脈に適した単語を１つ選択するタスクを学習させる際、圧倒的多数の負例（Negative Example）のうちの一部をランダムに標本化（Sampling）することで、［１］演算量の削減と、［２］正例／負例の割合不均衡の是正、を図ることが目的です。
つまり、Negative Sampling と Focal Loss が目指す方向性は概ね一致しており、前者が確率論的アプローチを、後者が決定論的アプローチをそれぞれ採用している、とも解釈できそうです。
以上をもちまして、RetinaNet の事例検討を終了します。次回から、また別のテーマに移ります。
↓ブログランキングに参加しています。よろしければ１クリックお願いします。
